【Processing】シグモイド関数でイージングを実装する

processing

はじめに

本記事では，Processingによるアート制作において，シグモイド関数を使ってイージングを実装する方法を紹介します．非常にお手軽にイージングを実装できるので，ぜひ使ってみてください．

シグモイド関数とは

シグモイド関数は

f(x) = \frac{1}{1+e^{-x}}

で表される関数で，グラフに書くと以下のようになります． eはネイピア数で，2.718...です．

f:id:gotutiyan:20201231111841p:plain
シグモイド関数の概形

desmosでの描画結果：https://www.desmos.com/calculator/64rtnb5z5i

定義域は無限で，値域が (0, 1)であるような関数です．ニューラルネットの活性化関数としてよく登場しますが，グラフの形からイージングに使えそうなことが分かります．

イージングのために使うことを考えると，-5でほぼ0（厳密には， e=2.718とすると 0.0066962987），5でほぼ1（厳密には， e=2.718とすると 0.9933037）となることは知っておくと良いと思います．

最も簡単な適用例

ここでは，円を左から右に移動するような動きに，シグモイド関数を使ってイージングをかけます．ひとまず，テンプレ+シグモイド関数がこちら．ネイピア数は2.718としています．

void setup(){
  size(500,500);
}

void draw(){
  background(0);
}

float sigmoid(float x){
  return 1/(1+pow(2.718, -x));
}

ここから，円を移動させることを考えます．今回は，60フレームかけて左端から右端へと移動させることにしましょう．ひとまず，コードは以下のとおりです．

void setup(){
  size(500,500);
}

void draw(){
  background(0);
  float sig_x = map(frameCount%60, 0, 59, -5, 5);
  float cir_x = map(sigmoid(sig_x), 0, 1, 0, width);
  circle(cir_x, height/2, 20);
}

float sigmoid(float x){
  return 1/(1+pow(2.718, -x));
}
  • sig_xは，シグモイド関数への入力です．フレーム数を60で割った余りは0から59なので，それをmap()を使って-5から5への範囲に変換します．なぜ-5から5にしたかというと，前述したとおり，シグモイド関数は-5でほぼ0，5でほぼ1をとる関数だからです．
  • cir_xは，円のx座標です．シグモイド関数は0から1の値を返すので，それをmap()を使って0からwidthに変換します．

実行例は以下のようになります．

f:id:gotutiyan:20201231112115g:plain

始点と終点の近傍では遅く，その中間では速くなるような動きが実現できています．

イージングの調整

上記の例では，シグモイド関数に-5から5への範囲を入力しましたが，この範囲を調整することで，機敏のあるイージングができるようになります．

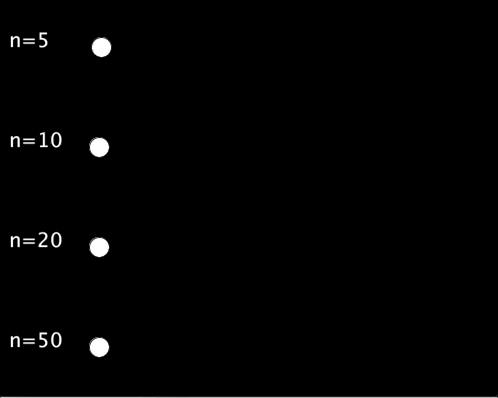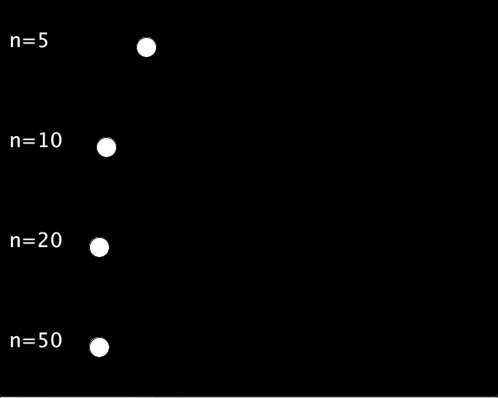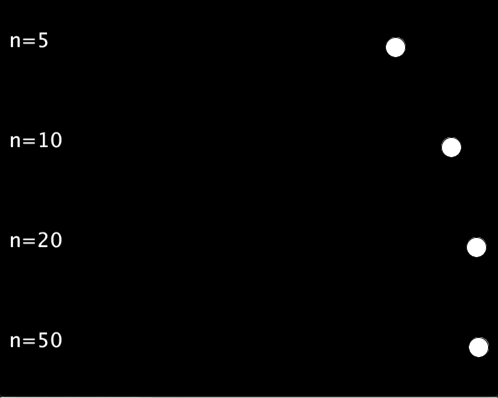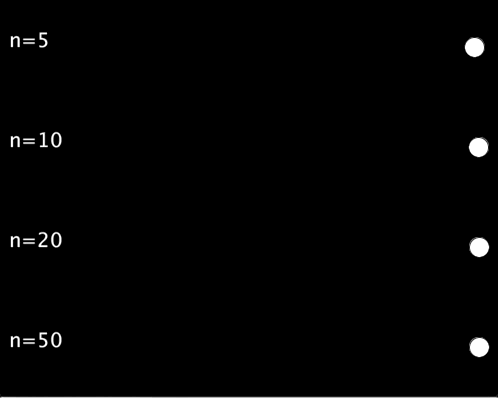
以下の例では，，シグモイド関数の入力として-5 ~ 5, -10 ~ 10, -20 ~ 20, -50 ~ 50の4種類を試しています．

void setup(){
  size(500,400);
  textSize(20);
}

void draw(){
  background(0);
  int n[] = {5, 10, 20, 50}; // 範囲の候補
  for(int i=0;i<4;i++){
    text("n="+n[i], 10, 50+100*i);
    float sig_x = map(frameCount%60, 0, 59, -n[i], n[i]);
    float cir_x = map(sigmoid(sig_x), 0, 1, 100, width-20);
    circle(cir_x, 50+100*i, 20);
  }
}

float sigmoid(float x){
  return 1/(1+pow(2.718, -x));
}

実行結果は以下のようになります．入力の範囲を広くすればするほど，待ち時間が長く，動き始めれば一瞬で移動するような動きになります．

f:id:gotutiyan:20201231113700g:plain

その他の適用例

イージングは様々な場面に適用できます．これまでに紹介した円の例では座標の動きにイージングをかけていますが，他の動きに適用する例を示します．

回転にイージング

シグモイド関数の返り値(0, 1)を(0, \pi /2)に変換して角度に使用してみます．

void setup(){
  size(500,200);
  rectMode(CENTER);
  textSize(20);
}

void draw(){
  background(0);
  int n[] = {5, 10, 20, 50};
  for(int i=0;i<4;i++){
    text("n="+n[i], 45+110*i, 130);
    float sig_x = map(frameCount%60, 0, 59, -n[i], n[i]);
    float rad = map(sigmoid(sig_x), 0, 1, 0,  PI/2);
    translate(50+120*i, 50);
    rotate(rad);
    rect(0, 0, 50, 50);
    resetMatrix();
  }
}

float sigmoid(float x){
  return 1/(1+pow(2.718, -x));
}

f:id:gotutiyan:20201231115618g:plain

図形の大きさにイージング

シグモイド関数の返り値(0,1)を(0, 50)に変換し，正方形の一辺の長さに使用します．

void setup(){
  size(500,200);
  rectMode(CENTER);
  noFill();
  stroke(255);
  strokeWeight(5);
  textSize(20);
}

void draw(){
  background(0);
  int n[] = {5, 10, 20, 50};
  for(int i=0;i<4;i++){
    text("n="+n[i], 30+110*i, 130);
    float sig_x = map(frameCount%60, 0, 59, -n[i], n[i]);
    float leng = map(sigmoid(sig_x), 0, 1, 0, 50);
    rect(50+110*i, 50, leng, leng);
  }
}

float sigmoid(float x){
  return 1/(1+pow(2.718, -x));
}

f:id:gotutiyan:20201231161755g:plain

おわりに

本記事では，イージングをシグモイド関数で実装する方法を紹介しました．