Hugging Faceを使った自作モデル作成の事始め
はじめに
Hugging FaceにはBertForClassificationなどの既存のモデルが定義されていますが,自作のアーキテクチャでモデルを定義・学習したいこともあります.本記事では,ある程度ちゃんとした形式で実装をするための事始めについて書きます.
本記事はpython3.11.0,および以下のモジュールで検証しました.
torch==2.1.0 transformers==4.34.0
概要
(HuggingFaceらしく)モデルを定義するためにはConfigとModelの2つのclassが必須です.
Configには,モデルを初期化および訓練するための情報を定義します.例えば,隠れ層のサイズや分類層の出力サイズ,もしくはdropoutの確率などです.
Modelは,Configさえ受け取れば初期化ができてforwardが通せるように設計します.例えば,configに入力次元数と隠れ次元数が書いてあれば,それを使ってLinearを初期化できます.
コードベースでは,ざっくり以下のようにモデルを初期化できればいいです.(ConfigとModelはそれぞれclassとして定義されていると思ってください)
config = Config() model = Model(config)
以下,色々な例を出しながら説明します.
最小限の自作モデルの実装例
まず手始めに,線形層を2層重ねただけのどうでもいいモデルを作ってみます. 入力は適当な5次元ベクトルで,隠れ次元数を3,出力は1次元のベクトルだとします(回帰タスクのつもりで).
Configの定義
Configを自作するときには,PretrainedConfigを継承する形で定義します.これにより,既に定義された変数が使えたり,セーブ・ロードがお手軽にできたり,transformersの既存Configとインターフェイスが合うなどの利点があります.
今回は2層積むので,入力サイズ,隠れサイズ,出力サイズの3つの情報があれば初期化できます.数値は適当です.
__init__()では必ずデフォルト引数を設定してください.
from transformers import PretrainedConfig class Config(PretrainedConfig): def __init__( self, input_size: int = 5, hidden_size: int = 3, output_size: int = 1, **kwards ): super().__init__(**kwards) self.input_size = input_size self.hidden_size = hidden_size self.output_size = output_size
(**kwardsはなんやねん,という方がいるかもしれません.PretrainedConfigにはどのモデルにも共通で使える(であろう)パラメータが既に多数定義されています.そのようなものについては,わざわざ自分でself.XXX =と書く必要はなく,**kwardsを経由してオーバーライドするだけで済みます.**kwardsの構文的な意味は,余った引数をまとめて辞書型で受け取ることです.その後,super().__init__(**kwards)で親クラスに(辞書を展開して)渡している感じです.構文的な意味についてはHuggin Faceではなくpythonの話なので,詳しくは検索してください.)
これで,Configのインスタンスを作ることができるようになりました.
config = Config() print(config) ''' printの結果: Config { "hidden_size": 3, "input_size": 5, "output_size": 1, "transformers_version": "4.34.0" } '''
もちろん,初期化のときに引数を与えれば好きな値を設定できます.
config = Config(
input_size=999,
hidden_size=1000,
output_size=999
)
print(config)
'''
printの結果:
Config {
"hidden_size": 1000,
"input_size": 999,
"output_size": 999,
"transformers_version": "4.34.0"
}
'''
また,PretrainedConfigはセーブ・ロードのメソッドを持っています.よく見るsave_pretrained()とfrom_pretrained()です.自作したクラスはPretrainedConfigを継承しているので,当然これらのメソッドを呼び出せます.
from_pretrained()はクラスメソッドであることに注意してください.
config = Config() outdir = 'sample' config.save_pretrained(outdir) loaded_config = Config.from_pretrained(outdir) print(config) print(loaded_config)
もしsave_pretrained()を呼んだ時にXXX.__init__() missing XX required positional arguments:のようなエラーが出る場合は,Configクラスの__init__()でデフォルト引数が設定されているか確認してください.
sampleディレクトリは勝手に作成されます.その中にconfig.jsonが保存されているので,中身を確認してみてください.
Configの定義は以上です.
モデル定義
モデルはPreTrainedModelを継承する形で定義します.冒頭でも述べたように,モデルは初期化の時にConfigを受け取るので,Configに書かれた情報を使いながら初期化するように__init__()を書きます.
from transformers import PreTrainedModel import torch.nn as nn class Model(PreTrainedModel): config_class = Config def __init__(self, config): super().__init__(config) self.config = config self.linear1 = nn.Linear( self.config.input_size, self.config.hidden_size ) self.linear2 = nn.Linear( self.config.hidden_size, self.config.output_size )
気をつけるべき点は以下です.
config_class = Configのように,クラス変数としてconfig_classにConfigを定義したクラスを設定してください.from_pretrained()でモデルを読み込む際に必ず必要になりますdef __init__(self, config):のように,初期化時にConfigのインスタンスを渡せるようにしてください..super().__init__(config)のように,親クラスの初期化のためにもconfigのインスタンスを渡してください.
こうすることで,以下のようにしてモデルを定義できます.次元数がConfigの通りになっていることを確認してください.
config = Config() model = Model(config) print(model) ''' printの結果 Model( (linear1): Linear(in_features=5, out_features=3, bias=True) (linear2): Linear(in_features=3, out_features=1, bias=True) ) '''
PreTrainedModelにセーブ・ロードのメソッドが定義されているので,これを継承した自作モデルはセーブ・ロードのメソッドを呼び出せます.Configの時と同じく,save_pretrained()とfrom_pretrained()です.
モデルをセーブする時にはConfigのsave_pretrained()も呼ばれるため,モデルをセーブすればConfigも勝手にセーブされます.
config = Config()
model = Model(config)
outdir = 'sample'
model.save_pretrained(outdir)
loaded_model = Model.from_pretrained(outdir)
もう一度sampleディレクトリを確認してください.モデルの重みを保存したファイルであるpytorch_model.binが保存されています.
あとはforward()を書けば完成です.forwardは学習ループの書き方にもよるのでかなり自由に書けますが,Hugging Faceらしい実装を目指すのであれば,
- forward()の引数にラベルを渡すことができて,ラベルを渡された時にはlossまで計算して返すようにする
- 返り値のために専用のOutputクラス(dataclass)を別に用意し,返り値はそれに入れて返す
をやっておくと良いと思います.
from transformers import PreTrainedModel import torch import torch.nn as nn from dataclasses import dataclass # 返り値用のクラス @dataclass class ModelOutput: loss: torch.Tensor = None logits: torch.Tensor = None class Model(PreTrainedModel): config_class = Config def __init__(self, config): super().__init__(config) self.config = config self.linear1 = nn.Linear( self.config.input_size, self.config.hidden_size ) self.linear2 = nn.Linear( self.config.hidden_size, self.config.output_size ) def forward( self, input, labels=None ): logits = self.linear1(input) logits = self.linear2(logits) loss = None if labels is not None: # labels=に何か与えられていたら損失計算 loss_fn = torch.nn.MSELoss() loss = loss_fn( logits, labels ) return ModelOutput( loss=loss, logits=logits )
こうすることで,次のように学習の1サイクルを回すことができます.
config = Config() model = Model(config) inputs = torch.rand((5)) # 何かの入力 labels = torch.tensor([0.5]) # 何かのラベル output = model(inputs, labels) print(output.loss) # tensor(0.9413, grad_fn=<MseLossBackward0>) output.loss.backward()
ここまで来たら,後はDataLoader周りを書けばいつも通り学習できます(この記事ではそこまでは踏み込みません).
既存モデルを組み合わせる場合の実装例(マルチタスク文分類を例に)
次に,既存モデル(例えばBERTなど)を組み合わせる場合の実装をしてみます.ここではマルチタスクの文分類をするような気持ちで,BERTなどのエンコーダから得られた表現を二種類の分類層に独立に入力するようなモデルを作りましょう.
要件は,
- 1つ目のタスクは2値分類.ラベルはA0, A1とする
- 2つ目のタスクは3値分類,ラベルはB0, B1, B2とする
- ドロップアウト層を分類層の直前に入れる
こととします.
Configの定義
モデルがConfigに書かれた情報だけで初期化できるようにConfigを定義しないといけないので,始めにどのような情報があれば初期化できるかを考えます.今回は,
- エンコーダとして使うモデルのid
- それぞれの分類タスクにおけるクラスのidとラベルのマッピング情報
- dropoutの確率
があれば良さそうです.(実際には,モデルを先に組んでみて,その後で必要な情報を含むようにConfigを定義するのも良いと思います)
実装としてはPretrainedConfigを継承して定義しますが,ここでPretrainedConfigがどのようなパラメータを既に持っているのか見てみます.以下のconfiguration_utils.pyのPretrainedConfigのソースがありますので,ざっと確認してみてください.
この中に既に使えそうなものがあれば自分で定義する必要はありません.今回はid2labelsとlabel2idがidとラベルのマッピング情報を表すので,これを片方の分類層のために使いましょう.それで,もう片方の分類層の情報は自分で定義しましょう.dropoutも自分で定義しましょう.
from transformers import PretrainedConfig class Config(PretrainedConfig): def __init__( self, model_id=None, id2label_second=None, label2id_second=None, dropout=0.1, **kwards ): super().__init__(**kwards) self.model_id = model_id self.id2label_second = id2label_second self.label2id_second = label2id_second self.dropout = dropout
初期化するときは,id2labelとlabel2idも忘れずに,計6つの引数を与えます. セーブとロードもできることを確認します.
config = Config(
model_id='bert-base-uncased',
id2label={0:'A0', 1:'A1'},
label2id={'A0':0, 'A1': 1},
id2label_second={0:'B0', 1:'B1', 2:'B2'},
label2id_second={'B0':0, 'B1':1, 'B2':2},
dropout=0.1
)
config.save_pretrained('out_test')
loaded_config = Config.from_pretrained('out_test')
print(config)
'''
printの結果:
Config {
"dropout": 0.1,
"id2label": {
"0": "A0",
"1": "A1"
},
"id2label_second": {
"0": "B0",
"1": "B1",
"2": "B2"
},
"label2id": {
"A0": 0,
"A1": 1
},
"label2id_second": {
"B0": 0,
"B1": 1,
"B2": 2
},
"model_id": "bert-base-uncased",
"transformers_version": "4.34.0"
}
'''
コンフィグの定義は以上です.
モデルの定義
次にモデルを定義します.Configの内容をうまく使いながら初期化していきます.
from transformers import PreTrainedModel, AutoModel import torch.nn as nn class Model(PreTrainedModel): config_class = Config def __init__(self, config): super().__init__(config) self.config = config self.transformer = AutoModel.from_pretrained( config.model_id ) hidden_size = self.transformer.config.hidden_size self.classifier = nn.Linear( hidden_size, len(config.id2label) ) self.classifier2 = nn.Linear( hidden_size, len(config.id2label_second) ) self.dropout = nn.Dropout(config.dropout)
モデルの初期化ができるか確認します.ついでにセーブとロードができるか確認します.
config = Config(
model_id='bert-base-uncased',
id2label={0:'A0', 1:'A1'},
label2id={'A0':0, 'A1': 1},
id2label_second={0:'B0', 1:'B1', 2:'B2'},
label2id_second={'B0':0, 'B1':1, 'B2':2},
dropout=0.1
)
model = Model(config)
model.save_pretrained('out_test')
loaded_model = Config.from_pretrained('out_test')
print(model)
'''
printの結果:
Model(
(transformer): BertModel(
.....中略.....
)
(classifier): Linear(in_features=768, out_features=2, bias=True)
(classifier2): Linear(in_features=768, out_features=3, bias=True)
(dropout): Dropout(p=0.1, inplace=False)
'''
最後にforwardを定義します.分類層が2つあるためラベルも2種類与えられるようにする点に注意します.また,BERTの入力を与える必要があるので,tokenizerの返り値をそのまま入力できるようにします.今回はかなりサボって,input_idsとattention_maskだけ受け取るようにしましょう.
from transformers import PreTrainedModel import torch import torch.nn as nn from dataclasses import dataclass class Model(PreTrainedModel): config_class = Config def __init__(self, config): super().__init__(config) self.config = config self.transformer = AutoModel.from_pretrained( config.model_id ) hidden_size = self.transformer.config.hidden_size self.classifier = nn.Linear( hidden_size, len(config.id2label) ) self.classifier2 = nn.Linear( hidden_size, len(config.id2label_second) ) self.dropout = nn.Dropout(config.dropout) def forward( self, input_ids, attention_mask, labels_first=None, labels_second=None ): logits = self.transformer( input_ids=input_ids, attention_mask=attention_mask ).pooler_output logits = self.dropout(logits) logits_first = self.classifier(logits) logits_second = self.classifier2(logits) loss = None if labels_first is not None and labels_second is not None: loss_fn = nn.CrossEntropyLoss() num_labels = len(self.config.id2label) loss_first = loss_fn( logits_first.view(-1, num_labels), labels_first.view(-1) ) num_labels = len(self.config.id2label_second) loss_second = loss_fn( logits_second.view(-1, num_labels), labels_second.view(-1) ) loss = loss_first + loss_second return ModelOutput( loss=loss, logits_first=logits_first, logits_second=logits_second )
最後に,適当な入力でforwardが通ることを確かめます.(本当は小さいデータで過学習するか,なども検証した方がいいですが割愛)
from transformers import AutoTokenizer config = Config( model_id='bert-base-uncased', id2label={0:'A0', 1:'A1'}, label2id={'A0':0, 'A1': 1}, id2label_second={0:'B0', 1:'B1', 2:'B2'}, label2id_second={'B0':0, 'B1':1, 'B2':2}, dropout=0.1 ) model = Model(config) tokenizer = AutoTokenizer.from_pretrained(config.model_id) # 何かの文 sentences = ['This is a sample sentence.', 'This is also sentence.'] encode = tokenizer(sentences, return_tensors='pt', padding='max_length') del encode['token_type_ids'] # 何かのラベル encode['labels_first'] = torch.tensor([0, 1]) encode['labels_second'] = torch.tensor([2, 1]) loss = model(**encode).loss print(loss) # tensor(2.1259, grad_fn=<AddBackward0>) loss.backward()
おわり
Hugging Faceを用いて自作モデルを作る方法について書きました.単純な線形層を積むだけのモデルから始まり,実際にBERTを用いてマルチタスクで文分類するモデルを実装してみました.
GECToR:系列ラベリングによる文法誤り訂正
GECToRは文法誤り訂正を系列ラベリングとして解くモデルです.既存の系列変換モデルに基づくモデルでは,入力文に対する訂正文をleft-to-rightに生成することで解かれてきました.一方,GECToRは系列ラベリングに基づいており,入力文を編集するような訂正方法になります.この記事では,GECToRの訂正手法からツールの動かし方までを解説します.
訂正手法
GECToRは入力文の各トークンに対して,訂正操作を示すタグを推定することで訂正します.推定されたタグは後処理として入力文に反映し,訂正文を獲得します.
タグ設計
GECToRが推定するタグはbasic-transformationとg-transformationの2種類に大別されます.
basic-transformationは,置換・挿入・削除・無編集の4種類の編集操作に基づくタグです.特に,置換および挿入のタグについてはどのトークンに置換するのか,どのトークンを挿入するのかという情報が必要ですので,トークンの情報も含めたタグになります(例:REPLACE_to,APPEND_the).そのため,削除と無編集のタグは1種類のみ(DELETE,KEEP)ですが,置換と挿入については複数存在します.
g-transformationは,言語情報に基づいたタグです.例えば,名詞のためには「単数形にする」「複数形にする」といったタグが存在し,動詞のためには「過去形にする」「現在形にする」などのタグが存在します.このようなタグは,語彙が異なっても同一のタグを推定すれば訂正できるため(apples→appleの訂正とbooks→bookの訂正は共に「単数形にする」というタグさえあれば訂正可能),クラス数の削減や,説明性の向上に寄与します.詳細は論文のAppendixのAにあります.
以下は論文中の例文を入力したときの訂正例です.$APPENDが挿入操作,$TRANSFORM_AGREEMENT_SINGULARが単数形にする操作,$TRANSFORM_VERB_VB_VBZが動詞に三単現のsをつける操作を示すものです.
入力文: A ten years old boy go school
----- Iteration 1 -----
A ten years old boy go school
$APPEND_- $TRANSFORM_AGREEMENT_SINGULAR $TRANSFORM_VERB_VB_VBZ
----- Iteration 2 -----
A ten - year old boy goes school
$APPEND_to
訂正文: A ten - year old boy goes to school
アーキテクチャ
BERTのようなEncoderの上に誤り検出とタグ推定のためのLinearが乗っている構造です.ただし,推論時には一度訂正して終わるのではなく,訂正文を再度入力することで反復的な訂正を行います(論文では2回程度訂正すれば十分だと報告されています).以下はTarnavskyi+22に記載の図であり,構造がわかりやすいかと思います.
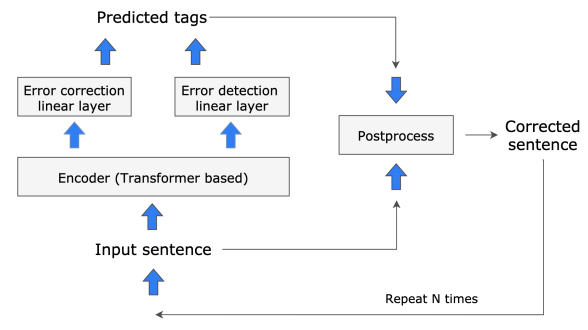
上の図からわかるように,GECToRはタグ推定とトークン単位の誤り検出確率推定のマルチタスクを解くように学習します. 両方の情報は訓練データから得られるため,その情報を教師として学習します.
マニア向け:推論時における誤り検出確率の使われ方
誤り検出確率は,反復的な訂正処理において,訂正を継続するかどうかを決定するために使われます.具体的には,誤り検出確率はトークン単位で推定しますが,その中の最大値が閾値より大きい場合に訂正が継続されます.
ここで閾値とは,推論時のパラメータとして定義されているものです.もし閾値を0に設定した場合,(NNの出力がぴったり0になることはない気がするので)検出確率に関わらず訂正は継続し,指定した反復回数に到達すれば推論が終了します.一方,もし閾値を0より大きくした時,指定した反復回数に到達するか,トークン単位の検出確率の最大値が閾値を超えなかった場合に推論が終了することになります.
ツールの動かし方
公式実装は以下です.
前処理
python utils/preprocess_data.py \ -s <誤り文のファイルパス> -t <正解の訂正文のファイルパス> -o <出力ファイルのパス>
誤り文と正解の訂正文を与えてタグの情報を事前に作ります.出力形式は入力のトークンとタグがSEPL|||SEPRで区切られたものが,さらに空白で区切られたものになります.
以下に例を示します.
echo 'I go to park a week ago .' > src.txt echo 'I went to the park a week ago .' > trg.txt python utils/preprocess_data.py -s src.txt -t trg.txt -o out.txt
このとき,out.txtは
$STARTSEPL|||SEPR$KEEP ISEPL|||SEPR$KEEP goSEPL|||SEPR$TRANSFORM_VERB_VB_VBD toSEPL|||SEPR$APPEND_the parkSEPL|||SEPR$KEEP aSEPL|||SEPR$KEEP weekSEPL|||SEPR$KEEP agoSEPL|||SEPR$KEEP .SEPL|||SEPR$KEEP
となります.これを試しに空白でsplitした後,各要素をさらにSEPL|||SEPRでsplitすると
[['$START', '$KEEP'] ['I', '$KEEP'] ['go', '$TRANSFORM_VERB_VB_VBD'] ['to', '$APPEND_the'] ['park', '$KEEP'] ['a', '$KEEP'] ['week', '$KEEP'] ['ago', '$KEEP'] ['.', '$KEEP']]
のようになって,タグが付与されていることがわかります.
訓練
--train_setや--dev_setには,上で紹介したutils/preprocess_data.pyの出力ファイルを指定します.
バッチサイズとかは調整してください.
python train.py \ --train_set <訓練データの前処理済みデータ> \ --dev_set <開発データの前処理済みデータ> \ --model_dir <モデル保存先のディレクトリ> \ --batch_size 64 \ --accumulation_size 4 \ --n_epoch 1 \
学習結果は以下のように保存されます(1エポックの場合).
model/
├── best.th
├── log
├── metrics_epoch_0.json
├── model_state_epoch_0.th
├── model.th
├── training_state_epoch_0.th
└── vocabulary
├── d_tags.txt
├── labels.txt
└── non_padded_namespaces.txt
もし特定の訓練済みモデルを読み込んでfine-tuneする場合には,--pretrain_folder,--pretrain,--vocab_pathを指定します.
# 特定のモデルを読み込んでfine-tuneする時 python train.py \ --train_set <訓練データの前処理済みデータ> \ --dev_set <開発データの前処理済みデータ> \ --model_dir <モデル保存先のディレクトリ> \ --batch_size 64 \ --accumulation_size 4 \ --n_epoch 1 \ --pretrain_folder <読み込むモデルのディレクトリ> \ --pretrain <読み込むモデルのファイル名(拡張子の.thは含めない)> \ --vocab_path <読み込むモデルに対応する語彙情報を有するディレクトリ>
例えば,上で示したようなディレクトリ構造においてmodel/best.thを読み込みたい場合には,
--pretrain_folder model \ --pretrain best \ --vocab_path model/vocabulary
のように指定します.
推論
python predict.py \ --model_path <読み込むモデルのパス(ファイル名まで含める)> \ --input_file <入力の生データ(前処理は不要)> \ --output_file <出力ファイルのパス> \ --vocab_path <読み込むモデルに対応する語彙情報を有するディレクトリ> \ --batch_size 64 \ --min_error_probability 0.0 \ --additional_confidence 0.0
推論時は,モデルのパスを拡張子まで含めて全て記述します.
--min_error_probabilityと--additional_confidenceは推論時に関係するハイパーパラメータです.--min_error_probabilityは誤り検出確率の閾値(マニア向けの節で説明しました)で,--additional_confidenceはKEEPタグのバイアスです.いずれのパラメータも値を高くするほど保守的な訂正になります.
また,アンサンブル設定で推論する場合には,--model_pathに複数のモデルを指定します.また同時に,--is_ensemble 1も指定する必要があります.
#NAIST定点観測部
NAIST Advent Calendar 2022の20日目の記事です.
#NAIST定点観測部は,NAISTの敷地を特定のポイントから撮影し,Twitterに投稿するときに使うハッシュタグです.部活としての実体はありませんが(ないですよね...?),代々有志により投稿が続けられています.
高山サイエンスタウンから物質棟の方面を見るような景観で写真を撮るのが主流です.階段は登りきってから,見下ろす形で撮るのが良さそうです.他にも,ガチ勢の中では階段は画面下に映らない方がよい,NAIST橋?は含めた方がよいなどの流派はあるようです.ここで,NAIST橋は,高山サイエンスタウンから食堂にかけて水路があり,そこにまたかがる小さな橋を指す造語のようです(以下のツイートの画像には,画面下部に良い感じにNAIST橋が写っています).
やざてんさんに細かく指導してもらって撮り直した!!!
— けんちょん (@drken1215) 2017年8月20日
NAIST橋が写真の下にあるくらいにするといいらしい!!#NAIST定点観測部 pic.twitter.com/1vIGr3rA8d
#NAIST定点観測部の他に#NAIST定点観測のハッシュタグも存在しますが,過去のツイートを参照する限りは#NAIST定点観測部と「部」をつけた方がメインです.少なくとも,最初の投稿日時は#NAIST定点観測部の方が先になっています.具体的には,2022年11月6日時点で現存する投稿の中で,最初の投稿日時は#NAIST定点観測部が2017年4月17日,#NAIST定点観測が2018年7月9日でした.(もちろん,すでに削除された投稿が存在して,本来の最初の投稿日時は異なるかもしれません.) ↓最初であろう#NAIST定点観測部↓
定点観測 #NAIST定点観測部 pic.twitter.com/YOr07V7RoB
— 春 (@HAL4hat) 2017年4月17日
いかがでしたか?#NAIST定点観測部の紹介でした.
ポエム:発表練習は3回くらいがちょうどいい
NAIST Advent Calendar 2022の7日目が空いていたので書きました.
スライドを使った口頭発表の練習は,3回くらいがちょうどいい.それより少ないと,「つなぎ」の発話がうまくできない.それより多いと,口が慣れ過ぎてしまう.
発表練習が少ないと,「つなぎ」の発話がうまくできない.いつもスライドの移り変わりの「つなぎ」になる部分の発話を意識している.スライドという発表形式は,内容こそ連続的であるが,視覚的には離散的である.N枚目とN+1枚目のスライドが視覚的に高くオーバーラップすることはあまりなく,視聴者からすると一瞬で内容が切り替わる(例え内容が連続であっても,少なくとも視覚的には変わる).発表者ができることは,その切り替わりができるだけ滑らかになるように,適切に「つなぎ」の言葉を入れることである.例えば,先行研究のスライドから問題点のスライドに切り替わる時に,「以上のような先行研究があるんですが,実は問題があります.」といった具合である.これにより,N枚目とN+1枚目のスライドの繋がりが分かりやすくなり,発表が聞きやすくなる(と思っている).もちろんスライドの作り方を工夫することでこんなことは考えなくても良いのかもしれないが,口頭でもサポートできるに越したことはない.発表練習が少ないと,この適切な「つなぎ」を上手く入れることができない.この原因は,発表者の視点に立った時,クリックもしくは矢印キーを押すことで,スライドがどのように変化するかを把握できてないことにある.スライドを切り替える時,切り替える直前に切り替えた後の様子が想像できないと適切な「つなぎ」は発話できない.スライドの順番を全て覚えろという主張ではない.でも,ある程度の流れは発表の途中でも予測しながら発表するべきである.このことは,発表に余裕が生まれるという副次的な利点にもつながる.これを達成するためには,発表練習はある程度必要である.
ただし,練習しすぎるのもダメである.練習しすぎると口が慣れ過ぎてしまう.口が慣れ過ぎると,次に何を話すかを決めるのが極めて容易になり,言葉の切れ目がなくなっていく.極端な話,原稿を丸覚えするような感じになる(原稿を作っていなかったとしても).やはり,覚えていることを単に口に出すよりは,覚える分量を減らし,代わりに言葉を逐次的に構築していく方がいい.この時に言い淀みや数秒の考える時間があっても構わない.個人的にはそうやって話してくれる方が好きである.また,口が慣れ過ぎると,「予定」とは違うことを話してしまった瞬間に崩れてしまう.練習すればするほど,あるスライドのある部分において自分が話す言葉は確立していき,固定化されていく.この固定化された言葉が「予定」である.そのような状態で「予定」とは異なることを万が一言ってしまうと,その場で少なからず混乱する.ここからの立て直しは多分難しい(し,立て直すような状況になりたくない).練習はしすぎるのもダメである.
やっぱり,発表練習は3回くらいがちょうどいい.
NAIST周辺のスーパーマーケット
はじめに
NAIST Advent Calendar 2022の5日目の記事です.
NAIST(広義?)周辺のスーパーマーケットを適当に紹介します.
- はじめに
- スーパーヤオヒコ 北大和店
- イオン登美ヶ丘店
- スーパーセンターオークワ 生駒上町店
- ラ・ムー 奈良二名店
- ラ・ムー 精華店
- MEGAドン・キホーテUNY精華台店
- 生鮮&業務スーパー 酒 ボトルワールドOK 押熊店
スーパーヤオヒコ 北大和店
NAIST最寄りのスーパー.野菜は普通で,肉魚は安めで良いものが多いと思います.魚に関しては刺身は綺麗だし,丸ごと一匹みたいな形式の品揃えもあって面白いです.肉に関しては鶏が強いと思います.もも・むね・ささみの代表的な部位だけではなくて,ハツやセセリみたいなマイナー部位も揃っており,イオンに比べると格安です.
惣菜関係では,ギガMAXチキンカツ弁当(名前の正確性に自信がないですが)というのが税込み258円なのでおすすめです(毎日あるわけではないらしく,何か法則があるのか検証中です).最近は大容量系の弁当もよく見かけます.
冷凍食品によく3割引みたいな表示がある気がしますが,割引後の価格がイオンと同じくらいなので特に安くは無いと思います.パンが3割引の日もあって,それはちゃんと安いです(多分月曜?).クレカ使えます.
イオン登美ヶ丘店
まあイオンは最強です.なんでもあります.NAISTからだと徒歩で20分ちょい,自転車で10分ちょいです.徒歩の場合,163号線沿いに歩いてお宝創庫手前の階段を上がる方が(両谷橋経由よりも)若干速いと思います.
野菜の売り場の入り口あたりのところに奈良県の産地直送コーナーみたいなところがあって,そこで小松菜や水菜が安くなっている時があります.肉魚は,18:30〜19:00あたりにかけて見切りが始まります.20時を過ぎるともう1段階安くなります(当然ながら品揃えとはトレードオフです).惣菜売り場の調理魚(パン屋の隣の位置)は19:00ごろに半額になる傾向があるのでおすすめです.
トップバリュ商品の缶のサイダーが30円ちょいでお勧めです.同じ種類のコーラはお勧めしません.
20日30日は5%オフです.イオンカードの支払いに限られるのでイオンカードを作りましょう.
スーパーセンターオークワ 生駒上町店
筆者が一回しか行ったことないので特に書くことがないです.価格は標準かちょっと高い印象です.広いので品揃えは問題なしです.缶のお酒のディスプレイの仕方がちょっと面白かったです.炭酸水が安いものがあります.
ラ・ムー 奈良二名店
ラ・ムーは肉が半端なく安いです.品質が心配になるレベルです(食べて体壊したことはないです).鶏豚は明らかに安く,牛もやっぱり安いと思います.ただ,どこのスーパーでも言えることですが,牛バラ肉の味付け肉はやっぱり脂が変でキツいので,お勧めしません.鶏肉のもろみ醤油の味付けはお勧めです.どう焼いても柔らかく仕上がります.
惣菜も安いです.唐揚げやコロッケなど充実しており,イオンなどと比べるとやはり破格です.個人的には鶏の山賊焼きというのがお勧めです.パンも安くて,ヤオヒコが3割引してる時の価格帯がデフォルトな感じの設定になっています(ちょっと言い過ぎかも).ヤマザキ春のパン祭りの時に価格あたりのポイントを最大化したい場合にはラ・ムー一択です.
デメリットはクレカが使えないことです.独自展開している大黒天payとかいうのを使えばキャッシュレスで支払いできます(現金でしか払ったことなし).
ラ・ムー 精華店
ラ・ムーつながりで精華町店も.特徴はほぼ奈良二名店と同じですが,お菓子の量り売りがあ流のが特徴です.
NAISTからの所要時間は,奈良二名も精華もそんなに変わらないと思います(真面目に測ったわけではないのですが).
MEGAドン・キホーテUNY精華台店
ラ・ムー 精華店をちょっと東に進むとメガドンキです.価格は標準的.肉は量り売りもやってるので,高めの肉を買いたい時にはちょうど良いはず.
関係ないですが,メガドンキの横のACADEMIA という本屋は,規模の割に技術書が充実しています(少なくともイオン登美ヶ丘店3階の本屋よりは).
生鮮&業務スーパー 酒 ボトルワールドOK 押熊店
ちょっと遠いですが,せっかくなので業務スーパーも紹介します.業務スーパーは冷凍食品が豊富な点が他のスーパーとは違います.カット野菜や海鮮,デザート系などの冷凍が安く売られています.ぷち大福シリーズの冷凍お勧めです.
押熊店はボトルワールドOKの系列なので,酒類も豊富です.割り材としてのペットボトル炭酸水や缶のジンジャエールもどちらも安いので(30~40円程度),合わせて買うと良さそうです.
論文メモ:ACL2022, Adjusting the Precision-Recall Trade-Off with Align-and-Predict Decoding for Grammatical Error Correction
Reference
@inproceedings{sun-wang-2022-adjusting,
title = "Adjusting the Precision-Recall Trade-Off with Align-and-Predict Decoding for Grammatical Error Correction",
author = "Sun, Xin and
Wang, Houfeng",
booktitle = "Proceedings of the 60th Annual Meeting of the Association for Computational Linguistics (Volume 2: Short Papers)",
month = may,
year = "2022",
address = "Dublin, Ireland",
publisher = "Association for Computational Linguistics",
url = "https://aclanthology.org/2022.acl-short.77",
pages = "686--693",
}
コード
概要
seq2seqな文法誤り訂正モデルのデコード手法として,precisionとrecallを制御するAlign-and-Predict Decoding (APD)を提案.デコードの各時刻で,入力をコピーするようなトークンの生成確率のみ変更することで制御する.入力をコピーするようなトークンは,入力文と出力途中の文とのアライメントを取れば分かる(ことがある).
背景
文法誤り訂正システムを使う目的によって,precision重視にするかrecall重視にするかは変わってきます.precisoin重視であれば,ユーザに間違いのない訂正を提示できるので,ユーザのexperienceは上がります.一方で,母語話者向けのシステムであればrecall重視の方がいいかもしれません.(参考:NLP2021 高再現率な文法誤り訂正システムの実現に向けて).
近年では,文法誤り訂正モデルにはseq2seqモデルとtaggerモデルの2種類が台頭しています.taggerモデルとして代表的なGECToRは,誤り検出確率の閾値とKEEPタグのconfidenceの2つのハイパーパラメタを用いることで,precisionとrecallのどちらを重視するかをある程度制御できます.一方,seq2seqモデルでも制御する方法は提案されているものの,多くはアーキテクチャやデータなど,特定の側面に依存していることが問題です.そこで,seq2seqのデコードの方法を改良することに注目した,Align-and-Predict Decoding (APD)を提案しています.
Align-and-Predict Decoding (APD)
直感
文法誤り訂正では,入力と出力がある程度一致することが多いです.seq2seqのような自己回帰モデルにおいては,デコードの過程で入力の部分系列と同じ系列を出力する状態が頻発します.
デコードの途中の状態を考えましょう.つまり,ある時刻までの系列は出力が完了しています.また,天下り的ですが,出力文のsuffix(接尾辞)が入力文のある部分系列と一致しているとします.このとき,次の時刻でモデルが入力をコピーする場合,どのトークンを選べばいいかは入力文から知ることができます.下図は自分で作ったものですが,仮にモデルが次の時刻でも入力をコピーするなら,入力文の部分系列(赤色)の右隣のトークン(青色)を持って来ればいいと分かります.
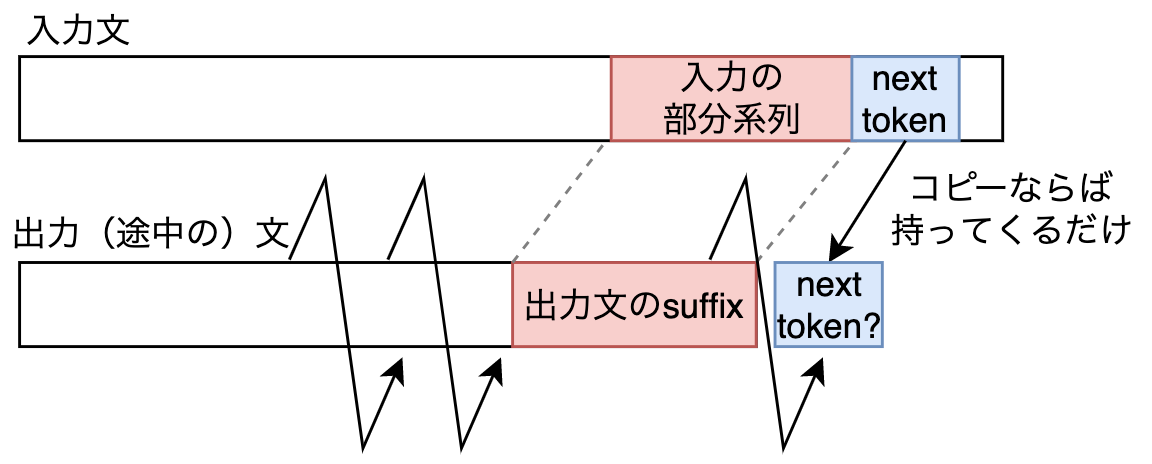
出力文のsuffixと入力文の部分系列で一致するものがあるかは,アライメントを取れば分かります.もしあれば,入力のコピーとなるトークンも分かります.したがって,コピーとなるトークンの生成確率のみを”いじる”ことが可能です.確率が高くなるようにすると,コピーが促進されて保守的な訂正になります(high-precison, low-recall).一方,その逆では積極的な訂正になります(low-precisoin, high-recall).
論文中の具体例に移ります.Figure1のBeam1では,最新の時刻においてwordを出力しており(suffixがword),入力文にもwordが存在します.したがって,次の時刻においてweが入力のコピーとなるトークンだと分かります.一方,weの生成確率は意図的に高くも低くもできるため(適当な値と積を取ればよい)コピーを促進するかどうかを制御できます.
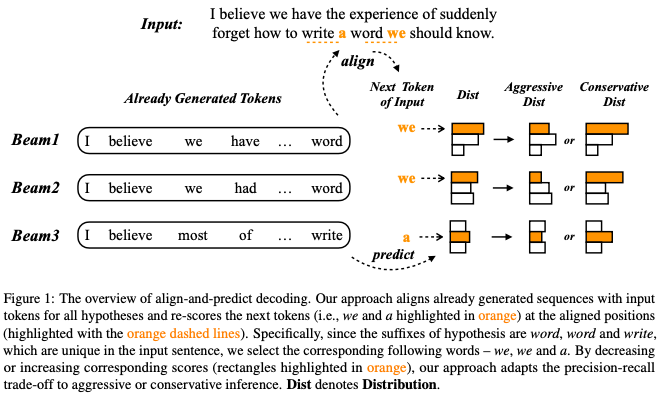
以上の考えをビームサーチにおけるそれぞれのビームに適用します.
式
厳密なnotationが欲しい人は論文を読んでください.
いま,ビーム幅のビームサーチをしており,時刻
まで出力が終了しています.
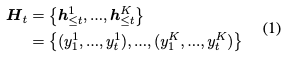
あるビームについて,出力済みの系列のsuffix(
)と一致する入力文の部分系列(
)が見つかれば,部分系列の次のトークン(
)を
に加えます.
は入力のコピーとなるようなトークンの集合です.
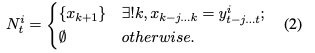
一旦話は普通のビームサーチに戻ります.とりあえず次の時刻のトークンとして全ての語彙を考えます.
![]()
top-kを取るために文のスコアリングをする必要があるので,次のようにスコアを計算します.普通のビームサーチと異なるのは,の重みの項がある点です.
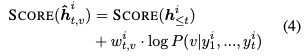
は,次のように決まります.
はハイパーパラメタです.
に属する語彙を出力するとコピーと同義になり,そのような語彙に対する重みが
です.
であれば積極的な訂正になり,
であれば保守的な訂正になります.(4)式は単に
の形である(マイナスしてない)ため,
の大小の解釈に注意します.
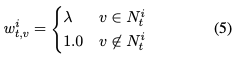
最後に,次の時刻のビームは,を考慮したスコアのtop-kを取ることで得られます.式中のarg topKは
と
に関係しているので,全てのビームと全ての語彙を考慮したtop-kになっています(普通のビームサーチと同じです).
![]()
実験と結果
実験は英語と中国語で行っています.詳しい実験設定は論文を参照してください.
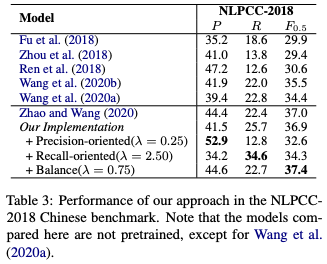
英語では,の値によってprecisionとrecallの制御が実現されていることがわかります.また,BARTで重みを初期化した場合(下図の最下ブロック)において,
に設定したときの
は先行研究を上回っています.
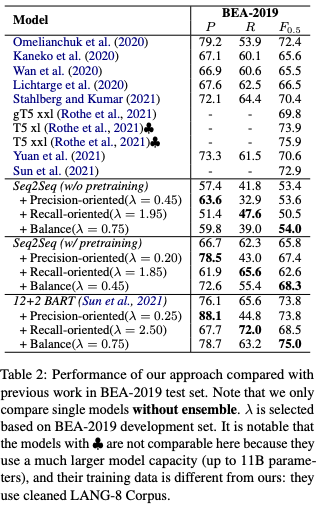
中国語での実験でも,の値によってprecisionとrecallの制御が実現されていることがわかります.
に設定したときの
は先行研究を上回っています.
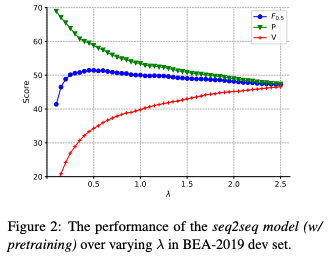
分析
の値によって,precision,recall,
がどのように変化するか調べています.データはBEA19共通タスクの開発データです.Figure2の結果は
が小さいほどhigh precision, low recallになっており,直感的です.
最後に,実例が示されています.の値が大きくなるほど,積極的に訂正していることが分かります.

感想
(2)式で出力文のsuffixと一致する入力文の部分系列を探すパートがありますが,ここで2トークン以上の部分系列が引っかかる場合があるのか気になりました.末尾Nトークンが一致するなら当然末尾N-1トークンも一致するので,再帰的に考えると末尾の1トークンが一致する場合しかないのではないかと思いました.言い換えると,(2)式のが1より大きくなるのか?と思いました.
デコードの時刻を進めるたびに入力文と比較するので,推論時間が長いのではと思いました.しかし,AppendixのBによると,5%長くなる程度のようで,そこまで影響ないようです.
を高くしてhigh precisionな出力を行った場合に,どの誤りタイプが多く訂正されるのかは気になりました.よりモデルが自信を持って推定できる誤りタイプは何か(逆に自信がない誤りタイプは何か),という分析に使えそうです.関連して,多様な訂正文の生成のためにも使えそうです.訂正文が多様になるように訓練していないモデルでも,APDを用いてデコードを工夫するだけで多様な訂正文が得られます.
関連研究
イントロでも触れましたが,Taggerモデルとして代表的なGECToRは,誤り検出の閾値とKEEPタグのconfidence(底上げする量)をハイパーパラメタとしています.これにより,コピーを促進するかどうかを制御できます.
誤り検出と誤り訂正を組み合わせる手法もあります [Chen+ 2020].はじめにスパンレベルの誤り検出を系列ラベリングとして解きます.その後,誤りがあると判断されたスパンのみに対して自己回帰モデルで訂正します.この方法では,誤り検出の確率に閾値を設定することで,コピーを促進するかどうかを制御できます(下記論文のTable 4).
論文ではreferされていませんが,[Hotate+ 2019]もprecisionとrecallの制御に言及しています.この手法では,訓練データを誤り率に応じて5段階にわけ,各段階に対応する特別なトークンを入力文にくっつけて訓練します.推論時には,所望の訂正率に応じて入力文の先頭に特別なトークンを付与して入力することで,訂正する度合いを制御できます.Table 3の結果では,特別なトークンとして誤り率が少なくなるようなものを付与したときほど,high-precisionおよびlow-recallの傾向にあることが報告されています.
GPT-2を使って文のパープレキシティを計算する
とある手法の再現実装をするために学んだので覚え書き.
transformersのGPT-2を使って文のパープレキシティ(perplexity)を計算するための実装について書きます.
フレームワークはPyTorch,python3.8.10で試しています.
インストール
# 仮想環境作るなら # python -m venv env # source env/bin/activate pip install torch transformers
一文のパープレキシティを計算
トークナイズ
訓練済みモデルを使うときは,語彙を揃えるために対応するトークナイザーを使います.transformersにはGPT-2のためのトークナイザーとしてGPT2TokenizerFastがあるので,これを使うことにします.モデルのIDにはgpt2を指定します.他にも,パラメータ数がより多いgpt2-largeなどが使えます.
from transformers import GPT2TokenizerFast model_id = 'gpt2' tokenizer = GPT2TokenizerFast.from_pretrained(model_id) sentence = ['This is a pen .'] inputs = tokenizer(sentence, return_tensors='pt', padding=True) print(inputs) # 出力:{'input_ids': tensor([[1212, 318, 257, 3112, 764]]), 'attention_mask': tensor([[1, 1, 1, 1, 1]])}
トークナイザーは文のリスト('str'オブジェクトのリスト)を入力とし,dictオブジェクトを返します(厳密には,一文ならリストにしなくてもいいです).返り値であるdictオブジェクトは2つの要素を含んでいます.一つはinput_idsで,トークンがIDに変換されたものです.もう一つはattention_maskで,バッチ化するときに使うものです.共にshapeは(バッチサイズ,系列長)です.
パープレキシティの計算
モデルにはtransformersのGPT2LMHeadModelを使います.トークナイザーと同じように,モデルのIDを指定して訓練済みのモデルをロードします.
from transformers import GPT2TokenizerFast, GPT2LMHeadModel import torch import math model_id = 'gpt2' tokenizer = GPT2TokenizerFast.from_pretrained(model_id) model = GPT2LMHeadModel.from_pretrained(model_id) sentence = 'This is a pen .' inputs = tokenizer(sentence, return_tensors='pt') with torch.no_grad(): outputs = model(input_ids=inputs['input_ids'], labels=inputs['input_ids']) print(torch.exp(outputs.loss)) # tensor(312.8972)
modelの返り値はCausalLMOutputWithCrossAttentionsオブジェクトです.入力のlabels=にinput_ids=と同じテンソルを渡すとlossが計算される仕組みになっています.lossは.lossで参照できます.これはtorch.Tensorオブジェクトなので,torch.exp() で囲むことでパープレキシティが得られます.
CausalLMOutputWithCrossAttentionsの詳細.
公式のページはここ: https://github.com/huggingface/transformers/blob/master/src/transformers/models/gpt2/modeling_gpt2.py#L1084
return CausalLMOutputWithCrossAttentions(
loss=loss,
logits=lm_logits,
past_key_values=transformer_outputs.past_key_values,
hidden_states=transformer_outputs.hidden_states,
attentions=transformer_outputs.attentions,
cross_attentions=transformer_outputs.cross_attentions,
)
このlossはクロスエントロピー損失で計算されます.
# 引用元:https://github.com/huggingface/transformers/blob/2c3fcc647a6d04f21668b1f5400c0fd33905bbb1/src/transformers/models/gpt2/modeling_gpt2.py#L1071 loss = None if labels is not None: # Shift so that tokens < n predict n shift_logits = lm_logits[..., :-1, :].contiguous() shift_labels = labels[..., 1:].contiguous() # Flatten the tokens loss_fct = CrossEntropyLoss() loss = loss_fct(shift_logits.view(-1, shift_logits.size(-1)), shift_labels.view(-1))
lm_logitsは(バッチサイズ,系列長,語彙サイズ)のshapeで,各トークンの生成確率が保存されています.lm_logits[..., :-1, :]とすることで,系列の最後尾以外の部分を抜き出しています. 一方,labelsは(バッチサイズ,系列長)のshapeで,labels[..., 1:]とすることで系列の先頭以外の部分を抜き出します.このように1トークンずらすことで,一般的なデコーディングの流れ(の推定結果を使って
を推定する流れ)を再現できます.
CrossEntropyLoss()はデフォルトのオプションでreduction='mean'が指定されているので,各トークンに対する損失の平均が計算されます.
複数文のパープレキシティを一度に計算(バッチ化)
バッチ化することで,複数文のパープレキシティを一度に計算することができます.基本的には上で述べた一文のみの場合と同じですが,トークナイズにpaddingの設定をする点と,クロスエントロピーの損失を計算するパートを若干自分で書く点が異なります.
トークナイズ
文によって文長が異なるので,バッチ化するときにはpadding=Trueを指定する必要があります.それから,トークナイザーの語彙にはいわゆるpad_tokenが設定されていないので,tokenizer.pad_token = tokenizer.eos_tokenとすることで追加しておきます.他にもtokenizer.add_special_tokens({'pad_token': '[PAD]'})とする方法もありますが,こうすると語彙サイズが1つ増えることでモデル側でindex out of rangeを起こして面倒なので,eos_tokenで代用します(実際,eos_tokenで代用するプログラムが多い印象です).
attention_maskを見ると,paddingされたトークンは,そうでないトークンは
であることが分かります.
from transformers import GPT2TokenizerFast, GPT2LMHeadModel import torch import math model_id = 'gpt2' tokenizer = GPT2TokenizerFast.from_pretrained(model_id) tokenizer.pad_token = tokenizer.eos_token model = GPT2LMHeadModel.from_pretrained(model_id) sentences = ['This is a pen .', 'This a is pen .', 'This is a pen pen pen pen .'] inputs = tokenizer(sentences, return_tensors='pt', padding=True) print(inputs['attention_mask']) ''' tensor([[1, 1, 1, 1, 1, 0, 0, 0], [1, 1, 1, 1, 1, 0, 0, 0], [1, 1, 1, 1, 1, 1, 1, 1]]) '''
パープレキシティの計算
モデルへの入力は基本的に一文のときと同じですが,attention_maskも追加で渡す点が異なります.しかしながら,三文を入力したのにもかかわらず,返り値のlossは一つの値になっています.これはlossの計算に使われているtorch.nn.CrossentropyLoss()のreduction=オプションが,デフォルトで'mean'になっているためです.'mean'では,文の境界にかかわらず,全てのlossが平均されて一つの値を返します.
model_id = 'gpt2' tokenizer = GPT2TokenizerFast.from_pretrained(model_id) tokenizer.pad_token = tokenizer.eos_token model = GPT2LMHeadModel.from_pretrained(model_id) sentences = ['This is a pen .', 'This a is pen .', 'This is a pen pen pen pen .'] inputs = tokenizer(sentences, return_tensors='pt', padding=True) with torch.no_grad(): outputs = model(inputs['input_ids'], attention_mask=inputs['attention_mask'], labels=inputs['input_ids']) print(outputs.loss) # tensor(6.3251)
そのため,outputs.logitsオブジェクトから自分でlossの計算を書きます.具体的には,torch.nn.CrossEntropyLoss(reduction='none')とすることで各トークンの損失を(平均など取ることなく)獲得し,dim=1で(つまり各文について)合計をとります.その後,それぞれの文の系列長で割ります.文の系列長は,attention_maskをdim=1で合計すると得られます(attention_maskは,pad_tokenでないトークンがとなっているため).
model_id = 'gpt2' tokenizer = GPT2TokenizerFast.from_pretrained(model_id) tokenizer.pad_token = tokenizer.eos_token model = GPT2LMHeadModel.from_pretrained(model_id) sentences = ['This is a pen .', 'This a is pen .', 'This is a pen pen pen pen .'] inputs = tokenizer(sentences, return_tensors='pt', padding=True) with torch.no_grad(): outputs = model(inputs['input_ids'], attention_mask=inputs['attention_mask'], labels=inputs['input_ids']) print(outputs.logits.shape) # torch.Size([3, 8, 50257]) # 1トークンずらす shift_logits = outputs.logits[:, :-1, :].contiguous() # 確率 shift_labels = inputs['input_ids'][:, 1:].contiguous() # 正解のトークンID shift_mask = inputs['attention_mask'][:, 1:].contiguous() # マスク batch_size, seq_len = shift_labels.shape loss_fn = torch.nn.CrossEntropyLoss(reduction='none') # reduction='none'に loss = loss_fn(shift_logits.view(-1, shift_logits.size(-1)), shift_labels.view(-1)).view(batch_size, seq_len) print(loss.shape) # torch.Size([3, 7]) # shift_maskと積をとることで,pad_tokenに対する損失を無視する. # shift_mask.sum(dim=1)とすることで,各文のpad_tokenを除いた系列長が得られる loss = (loss * shift_mask).sum(dim=1) / shift_mask.sum(dim=1) print(torch.exp(loss)) # tensor([ 312.8972, 3360.7671, 125.8699])