論文メモ：COLING2016, Automatic Extraction of Learner Errors in ESL Sentences Using Linguistically Enhanced Alignments

論文メモ 
@inproceedings{felice-etal-2016-automatic,
    title = "Automatic Extraction of Learner Errors in {ESL} Sentences Using Linguistically Enhanced Alignments",
    author = "Felice, Mariano  and
      Bryant, Christopher  and
      Briscoe, Ted",
    booktitle = "Proceedings of {COLING} 2016, the 26th International Conference on Computational Linguistics: Technical Papers",
    month = dec,
    year = "2016",
    address = "Osaka, Japan",
    publisher = "The COLING 2016 Organizing Committee",
    url = "https://aclanthology.org/C16-1079",
    pages = "825--835",
}

この論文は，Copyright © 1963–2021 ACL，Creative Commons Attribution 4.0 International Licenseの下で公開されています．

概要

文法誤り訂正（GEC）のための自動アライメント手法を提案しました．特に，Damerauの編集距離をベースとし，言語情報を考慮することでコストの計算部分を拡張します．また，2トークン以上の編集にも対応させるために，アライメントをマージする手法も提案します．人手のアライメントと比較する実験の結果，提案したアライメント手法は人と80%以上一致することを示唆しました．さらに，ルールベースに基づく手法であるため，編集情報の抽出を一貫性をもって行えるとしています．

自動アライメントの重要性

今までは，アライメントは手動で行われることが一般的でした．しかし，手動のアライメント手法には次の2点の問題点があると主張しています．また，自動のアライメント手法ではこれらを解決できるとしています．

  1. アライメント作業は面倒
    直感的にも，手動アライメントは面倒な作業です．edit-basedな評価を行うことを考えると，原文とモデルの出力文に対してのアライメントを毎回取る必要があります．これを毎回人手で行うわけにはいかないため，自動アライメント手法を確立することは重要です．

  2. 一貫したアライメントが取れない
    手動のアライメントは一貫性がないことがあります．人手で行われたアライメントを分析すると，[has → was] というアライメントもあれば，[has eating → was eating]というアライメントもあったようです．後者の例ではeatingという単語は変化していないため，[has → was]のみにした方が良さそうに見えます．自動アライメントではこのような違いは発生せず，一貫性のあるアライメントが取得できます．

アライメント手法

まず，大きな枠組みとしてDamerauの編集距離のコストからアライメントを取ります．Damerauの編集距離は，置換，挿入，削除，隣同士の単語の入れ替えを許す編集距離です．今まではノーマルなLevelshtein Distanceが用いられてきましたが，語順誤りにはうまく対応できませんでした．例えば，[A B → B A]のような訂正の場合，[A → \phi]，[B → B]，[\phi → A]のように3つのアライメントに分かれてしまいます．そこで，入れ替えの操作も許すDamerauの編集距離を採用することで，語順入れ替えも「語順入れ替え」として処理できるようになりました．さらに，[A B C → B C A]のような3トークン以上の語順入れ替えに対応するために，コスト行列を対角線的に遡って探索するように拡張しています（Listing 1）．

f:id:gotutiyan:20210810005636p:plain

次に，Damerauの編集距離の置換コストを，言語情報を考慮したものに置き換えます（Listing 2）．考慮する言語情報は次の4つです．

  1. 小文字化したときに一致するか
    一致すればコストは 0とします．そうでなければ，次の2. 3. 4. の3つのコストを足した値とします．

  2. lemma cost
    metとmeetingのように，置換前後の単語が同じlemmaを持つ，もしくは派生形（derivationally related form）であれば 0，そうでなければ 0.499とします．

  3. part-of-speech cost
    置換前後の単語が同じ品詞なら 0，ともに内容語（形容詞，副詞，名詞，動詞）なら 0.25，いずれでもないなら 0.5とします．

  4. character cost
    置換前後の単語の文字レベルのDamerau-Levenshtein distanceを，アライメントの長さで割った値とします（ 0 〜 1）．

lemma costでは派生形（derivationally related form）という概念があります．ここで派生形は，置換前後のトークンのlemma集合が交差していることを指します．例えば，metとmeetingが派生形かどうか調べたいとして，各単語のlemma集合を考えます．metは動詞のみなのでlemmaはmeet，meetingは名詞と捉える場合と動詞と捉える場合でlemmaが異なり，それぞれmeeting，meetです．よって，lemma集合はそれぞれmeetとmeeting, meetであるので交差し，2つの単語は派生形とみなされます．

f:id:gotutiyan:20210810000125p:plain

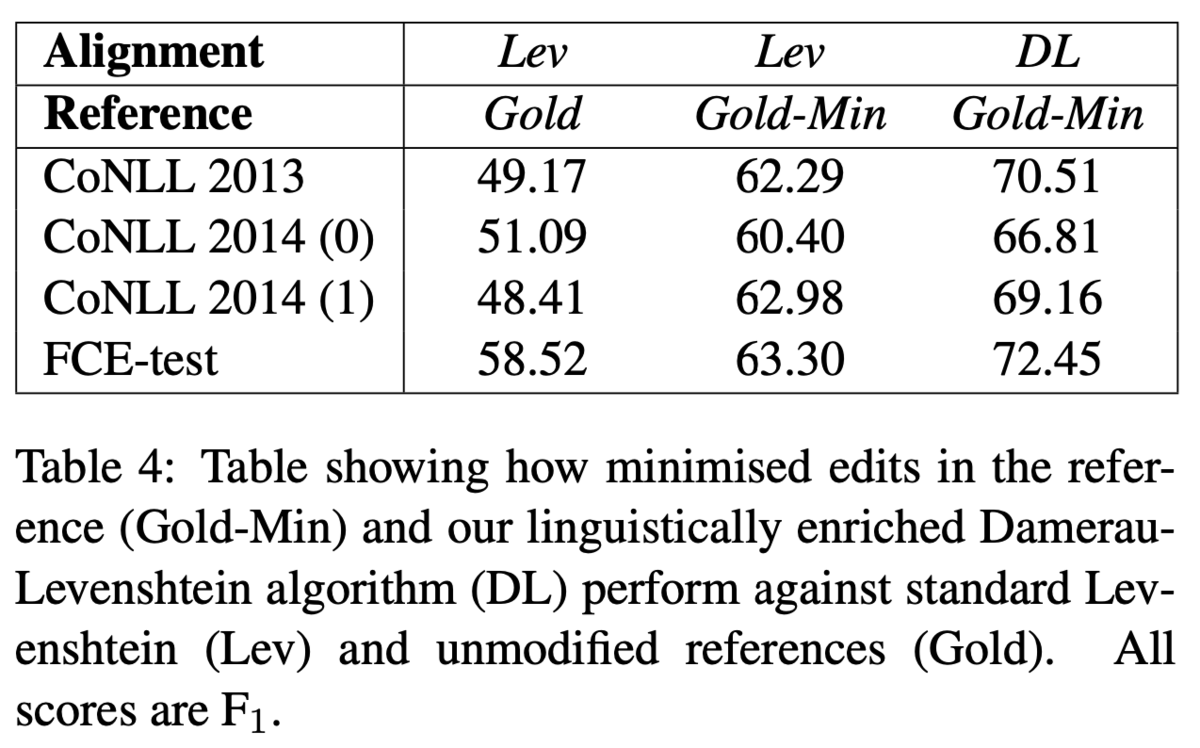
実験

自動アライメントと手動アライメントを比較し， F _ 1スコアを見る実験を行っています（Table 4）．まず，Levenshtein Distanceによるアライメントと，人手で作成したGoldアライメントは50%程度の F _ 1スコアでした（Table 4，LevとGoldの列）．

次に，人手アノテーションを最小限の訂正になるように修正したアライメントも作成しました．具体的には，両端から同じトークンを再帰的に削除します．この処理により，[has eating → was eating]のような訂正も[has → was]のみになります．このように修正を加えたGoldをGold-Minと呼んでいます．このデータを用いると，Levenshtein Distanceでは60%程度の F _ 1スコア，Damerauの編集距離だと70%程度の F _ 1スコアでした．この結果から，アライメントの最小化を行う処理はアライメントをより正しく評価することができ，かつ，言語情報を取り入れたDamerau編集距離が人との一致率の向上に貢献することがわかります．

f:id:gotutiyan:20210810003127p:plain

アライメントのマージ

これまでに説明されたアライメントの手法では，2トークン以上の編集が分割されることがあります．人手のアノテーションを見ると，ほとんどの編集は0:1（1トークンを挿入），1:1（1トークンを別の1トークンに置換），1:0（1トークンを削除）のいずれかですが，0-2:0-2のような訂正もやはり存在します（Table 6）．よって，得られたアライメントを適切にマージする必要があります．例えば，[wide spread → widespread]のように結合するような編集は，現状のアルゴリズムでは[wide → widespread]，[spread → \phi]のように，1:1と1:0の2つの編集に分割されます（Table 5）．このようなものはマージして[wide spread → widespread]とし，2:1の編集として扱う方が望ましいです．

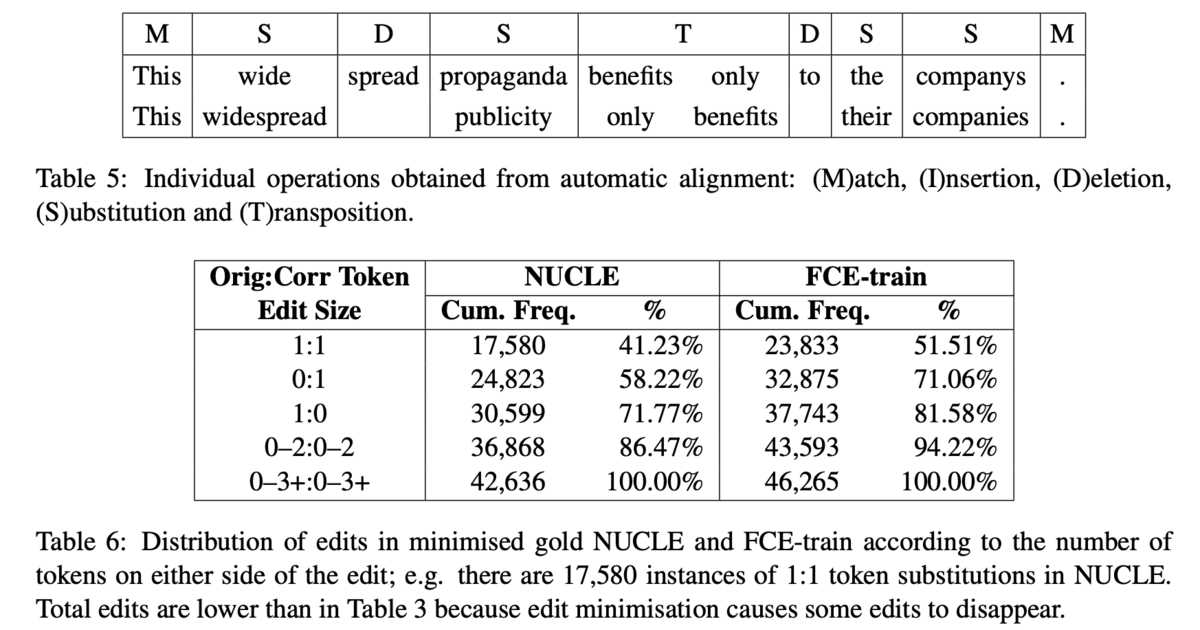
f:id:gotutiyan:20210810152834p:plain

アライメントのマージは10個のルールに基づいて行います．（このルールに関しては，論文の記述を直接読んだ方が分かりやすいと思います．以下は参考程度で．）

  1. 挿入アライメント（M）で分割する． 例：アライメント列がMSDSTDSSMなら，M, SDSTDSS, M

  2. 句読点を含む編集で，その次にケース変更の編集があればマージする．
    例：[, → .]，[we → We]があれば，[, we → . We]

  3. 入れ替えの編集があれば，それを独立にする．

  4. 所有格の接尾辞に関する編集は，その前の編集とマージする．
    例：[friends → friend]，[\phi → 's]があれば，[friends → friend 's]

  5. トークンの間に空白を挿入もしくは削除する編集をマージする．

  6. 文字が70%より多く一致している単語で，かつ，その前のトークンと品詞が一致していなければ独立にする．

  7. ある置換の編集の前に置換の編集があるとき，独立にする．

  8. 少なくとも一つの内容語が含まれる編集の組み合わせを全てマージする．

  9. 同じ品詞に関する連続した編集をマージする．

  10. 連続した編集の最後にある決定詞に関する編集は独立にする．

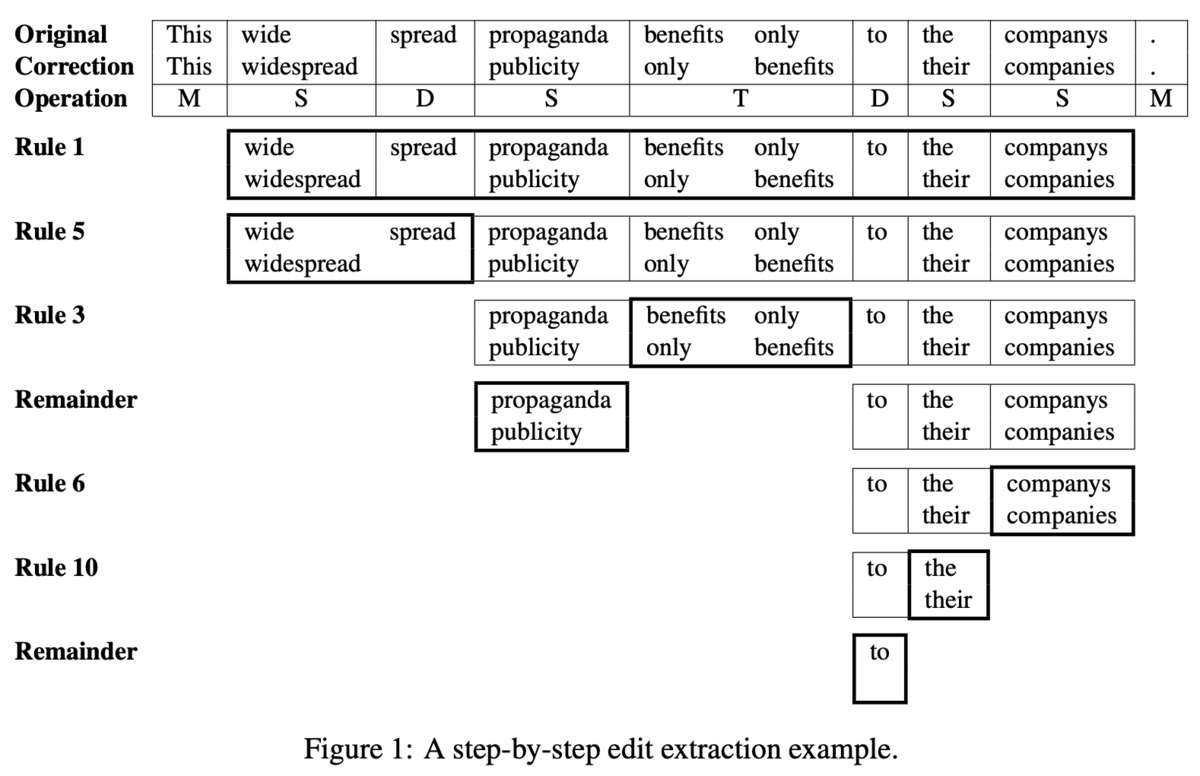
これらのルールは1>2>...>10の優先度で適用されます．また，あるルールを適用してマージ・分割が起これば，残りの未確定の部分列に対して再帰的に適用されます．Figure 1はその一例です．

f:id:gotutiyan:20210810161230p:plain

アライメントのマージに関する実験

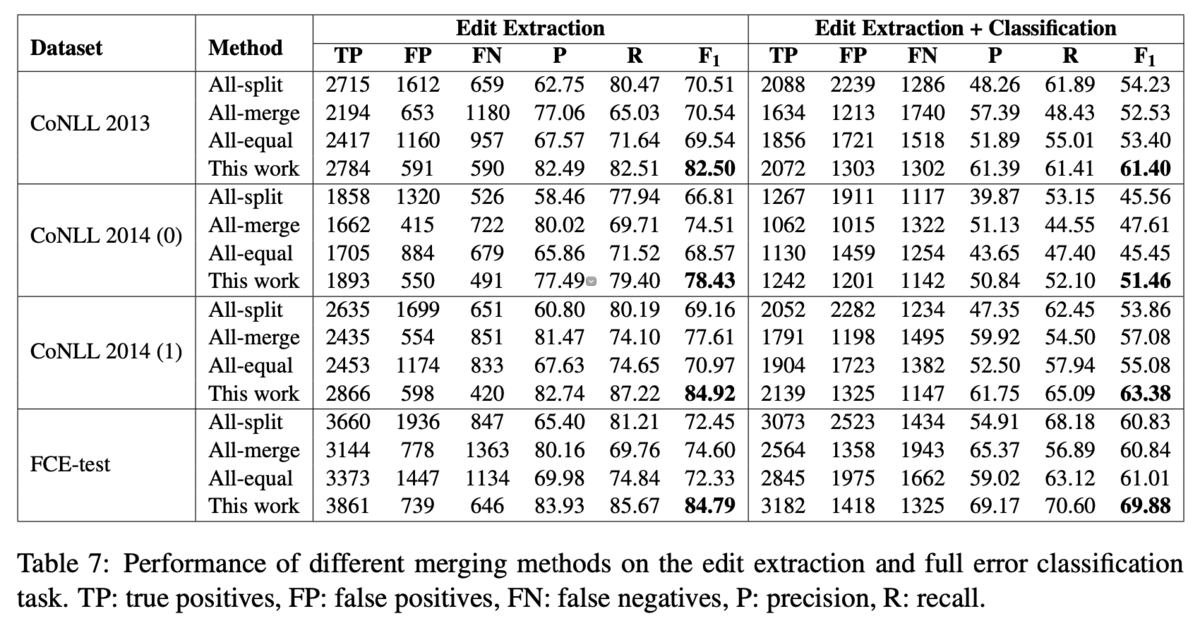
アライメントをマージすることで，さらに人との一致率が向上することが示唆されました．ベースラインとして，All-split（マッチしないアライメントは全て独立にする），All-merge（マッチしない連続したアライメントは全てマージする），All-equal（同じ操作であって，マッチしない連続したアライメントはマージする）の3つと比較しています．

結果はTable 7の通りです．提案手法が最も高い一致率を示しました．ただし，ベースラインの手法にはそれぞれ良いところがあるとしています．例えば，All-splitはTPは高くFNは低いが，FPも高くなります．これは2トークン以上に関わる訂正を無視するような設定になっているからです．一方で，All-mergeはFPの値が低くなる一方でTPは低く，FNは高くなります．提案手法はルールベースな手法によりアライメントを適切に分割・マージするので，All-splitとAll-mergeの良いところを利用できるため，一致率が高くなると分析しました．

それから，エラータイプの分類も考慮した一致率でも，提案手法は最も高い値を示しました．編集情報へのエラータイプの付与は，MaxEnt error type classifierを利用したとしています．

f:id:gotutiyan:20210810162830p:plain

考察

ここまでに行ってきたアライメントの性能評価は，どうしても過小評価されています．例えば，同じ編集でも，人によって[has eaten → was eating]，もしくは[has → was] + [eaten → eating]のようにバラつくことがあります．このようなばらつきは最小化（Gold-Minを作ること＝端から一致したトークンを消すこと）を実施しても解消されないため，自動アライメントはいずれか一方にしか正解の判定を得られません．

他のデメリットとして，複数の誤りを扱う編集や，編集の途中に未編集のトークンが存在する訂正はうまくマッチしないことがあります．（Gold-Minは両端からのみ未編集のトークンを消すので，途中に存在する未編集トークンは最小化できない．）

一方でメリットは，出力に説明性があること，一貫性があることです．ある編集がマージ・分割された理由を知りたいときは，その操作を実施したルールから説明できます．また，ルールベースに基づいているので，編集の抽出に一貫性があります．

最後に，自動アライメントの先行研究と比較し，提案手法がF1スコアを大きく上回っていることを示しました（Table 8, 9，本記事では割愛）．